mercredi, 23 février 2022
À la mémoire de l'académicien Igor Rostislavovich Shafarevich

À la mémoire de l'académicien Igor Rostislavovich Shafarevich (Chafarevitch)
par Arkady Minakov
Source: https://www.geopolitica.ru/article/pamyati-akademika-igorya-rostislavovicha-shafarevicha
Le 19 février 2022, cela fera cinq ans qu'Igor Rostislavovitch Shafarevich est décédé. Il était sans aucun doute l'une des figures clés de la société russe du dernier tiers du XXe siècle et du début du XXIe siècle.
On ne peut pas dire que son nom soit peu connu de nos jours, mais peu de choses sont dites et écrites à son sujet dans l'espace public. Il y a de très bonnes raisons politiques à cela, pour lesquelles la figure de Shafarevich dans les années 1980 a été négativement mythifiée et tabouisée dans les médias libéraux.
Shafarevich est né le 3 juin 1923 à Zhytomyr. Son père, Rostislav Stepanovich, est diplômé du département de physique et de mathématiques de l'université d'État de Moscou et a travaillé comme professeur de mécanique théorique. Shafarevich se souvient : "L'origine de mon père n'est pas très claire. C'est-à-dire qu'il est lui-même originaire de Zhytomyr, mais d'où viennent ses parents - pas très clair pour moi. La racine "Shafar" elle-même figure dans le dictionnaire des racines slaves du Sud ou slaves de l'Ouest. J'ai rencontré un tel nom de famille dans des références à un auteur polonais, et on le trouve également en Serbie. Selon les rumeurs familiales, mon grand-père venait de Serbie. Cette conclusion est tirée d'abord du fait qu'il était orthodoxe (il était sacristain dans une église), et ensuite qu'il venait de l'Ouest : il parlait russe avec un accent. Et quel autre Occident orthodoxe y a-il? ...".
Sa mère, Yulia Yakovlevna, philologue de formation, ne travaillait pas la plupart du temps. Son père était le directeur de la succursale de la ville d'une banque d'État. Shafarevich se souvient : "C'était une occupation très dangereuse, car les premières troupes qui arrivaient prenaient tout l'or, et les suivantes exigeaient qu'il le donne. Plusieurs fois, il a été emmené au peloton d'exécution".
Certaines des terribles réalités des années post-révolutionnaires se sont fermement ancrées dans l'esprit du garçon : "... j'ai assisté à la tragédie de la paysannerie russe. Mes parents louaient la moitié d'une cabane de paysans en été au lieu d'une datcha (et les paysans déménageaient dans l'autre moitié). Elle se trouvait non loin de la ville actuelle de Pushkino. Le village s'appelait Kuronovo. Il n'existe plus - le terrain sur lequel il se trouvait a été inondé par le réservoir. Je me souviens que des choses étranges se sont produites lors de la construction du réservoir. Pendant la journée, mes amis et moi jouions aux raiders cosaques sur la rive, en nous cachant dans les buissons, et le soir, des personnes qui me semblaient énormes, à moi, un enfant, en raison de la différence de taille, ont été conduites dans les buissons. Des chiens aboyeurs les gardaient. Je n'ai pas communiqué avec eux, j'ai juste vu cette image d'une masse sombre s'étendant devant notre maison".
Les parents de Shafarevich lui ont donné une excellente éducation, il connaissait plusieurs langues et était extrêmement cultivé pour son âge. Déjà dans sa maturité, il a dressé une liste de vingt livres, qui lui ont fait "la plus grande impression". Parmi eux figuraient les byliny russes, les contes d'Afanasiev, des frères Grimm, Le Prométhée enchaîné et les Euménides d'Eschyle, l'Histoire d'Hérodote, le Faust de Goethe, Pouchkine et Dostoïevski. Ces livres lui ont très probablement été lus lorsqu'il était enfant.
Le cercle de lecture de Shafarevich s'est considérablement enrichi d'ouvrages de fiction moderne, d'ouvrages historiques, philologiques et philosophiques : des livres de Soljenitsyne (Un jour dans la vie d'Ivan Denisovitch, Le Pavillon des cancéreux, L'Archipel GULAG), des "rednecks" de V.I. Belov ("Kanun") et autres. I. Belov ("Eve"), V. G. Raspoutine ("Adieu à la mère"), études de la mythologie, de la littérature et de la culture russes anciennes, ouvrages sur l'histoire de la société occidentale et russe. Une place spéciale dans cette liste a occupé les livres des penseurs conservateurs russes I.A. Ilyin "Sur la monarchie et la république" et "Nos tâches" ; I.L. Solonevich "Narodnaya Monarchiya", L.A. Tikhomirov "L'État monarchique".

À l'école, Shafarevich a développé un intérêt très profond pour l'histoire (il avait même l'intention de devenir historien, mais a ensuite considéré à juste titre que dans l'URSS extrêmement idéologisée, l'étude professionnelle de l'histoire entraînerait un coût moral et intellectuel trop important). Finalement, il a opté pour les mathématiques.
Dès l'âge de treize ans, il suit le programme scolaire en mathématiques, puis le programme de la faculté de mécanique et de mathématiques de l'université d'État de Moscou, où il passe ses examens externes. En huitième année, le jeune homme phénoménalement doué a suscité l'intérêt des professeurs du MGU (B. K. Delaunay), et en neuvième année, Igor Shafarevich a commencé des travaux de recherche en algèbre et en théorie des nombres. Après avoir quitté l'école, il est accepté en dernière année de la faculté de mécanique et de mathématiques et obtient son diplôme en 1940, à l'âge de 17 ans. Shafarevich a soutenu sa thèse de doctorat à l'âge de 19 ans et sa thèse de doctorat à l'âge de 23 ans. Il a rejoint la faculté du département de mécanique et de mathématiques de l'Université d'État de Moscou en 1944, et à partir de 1946, il a intégré le personnel de l'Institut mathématique Steklov (MIAN). Il a supervisé la soutenance de plus de trois douzaines de thèses de doctorat. En 1958, Shafarevich a été élu membre correspondant de l'Académie des sciences de l'URSS et en 1991, il a été élu membre de l'Académie des sciences de Russie. Il a reçu le prix Lénine en 1959 pour la découverte de la loi générale de réciprocité et pour avoir résolu le problème inverse de la théorie de Galois. Les principaux travaux de Shafarevich portaient sur l'algèbre, la théorie des nombres et la géométrie algébrique. Il était l'un des mathématiciens les plus connus de notre époque, et membre des principales académies et centres scientifiques étrangers.

Shafarevich percevait les mathématiques comme "une belle symphonie se poursuivant sans fin", et l'opportunité de s'y évader du monde des dictats idéologiques, son "sens et sa beauté l'ont amené à réaliser le but religieux de la connaissance du monde". Lors d'une conférence prononcée à l'occasion de la remise du prix Heinemann en 1973 à l'Académie de Göttingen, Shafarevich a particulièrement insisté sur la relation entre la religion et les mathématiques, accordant une nette priorité à la religion : "Ce n'est pas la sphère la plus basse en comparaison, mais la plus haute de l'activité humaine - la religion - qui peut donner un but aux mathématiques. <...> Les mathématiques ont été formées en tant que science au 6e siècle avant J.-C. dans l'union religieuse des Pythagoriciens et faisaient partie de leur religion. Les mathématiques avaient un objectif clair : c'était un moyen de fusionner avec le divin en comprenant l'harmonie du monde exprimée dans l'harmonie des nombres. <...> Je voudrais exprimer l'espoir que, pour la même raison, il peut maintenant servir de modèle pour la solution du principal problème de notre époque : trouver un but religieux plus élevé et le sens de l'activité culturelle de l'humanité.
En l'absence d'un objectif religieux supérieur, toute l'activité scientifique de l'humanité ne mène qu'à la destruction globale.
Cependant, ce ne sont pas seulement ses succès en mathématiques qui ont rendu Shafarevich célèbre dans le pays et dans le monde. En tant que mathématicien, il reste connu d'un cercle relativement restreint de professionnels. Son activité sociale et politique dans le cadre du mouvement dissident, qui a vu le jour en URSS à cette époque, lui a apporté une notoriété incommensurable. Dès 1955, il a signé la "Lettre des trois cents" adressée au Comité central du Parti communiste de l'Union soviétique en solidarité avec la protestation des biologistes contre Lyssenko. En 1968, il a signé une lettre collective pour défendre le militant dissident des droits de l'homme A.S. Yesenin-Volpin, qui était emprisonné dans un hôpital psychiatrique. Et dès la fin des années 1960, Shafarevich devient l'un des leaders du mouvement dissident, rejoignant le "Comité des droits de l'homme en URSS" organisé par A.D. Sakharov, créé fin 1970, où il fait de la protection des droits des croyants l'un des thèmes principaux. Shafarevich occupait une position particulière au sein du Comité : "J'étais membre du Comité, mais j'étais irrité par le manque de direction dans ses activités. Il me semblait inutile d'étudier la situation des droits de l'homme en URSS, et non de se battre pour eux. J'ai rédigé un rapport sur l'état des religions en URSS. En préparant le rapport, j'ai souligné que la persécution anti-religieuse se produit dans tous les pays socialistes, sans exception. Partout où le socialisme s'est manifesté, que ce soit en Albanie, en Chine, partout les mêmes événements ont eu lieu : persécution de toute confession existante, persécution des croyants, quelle que soit leur croyance. Cela m'a fait réfléchir à la nature du socialisme lui-même.

Shafarevich a exposé sa vision du socialisme, remarquable par la profondeur et la clarté de sa compréhension, dans un court article intitulé "Socialisme", publié dans la collection "De sous les rochers", conçue par lui et A.I. Solzhenitsyne comme une sorte de continuation des célèbres collections "Jalons" et "De profondeur". Shafarevich a présenté le socialisme comme une conséquence des grandes crises vécues à plusieurs reprises par l'humanité. Le socialisme en tant que théorie et pratique est une manifestation du désir d'autodestruction de l'humanité, du Néant ; il est hostile à l'individualité, relègue l'homme au niveau des détails d'un organisme étatique et cherche à détruire les forces qui soutiennent et renforcent la personne humaine : la religion, la culture, la famille, la propriété individuelle.

Immédiatement après l'arrestation et la déportation hors d'URSS de son co-auteur Soljenitsyne en février 1974, Shafarevich a écrit des lettres ouvertes pour défendre l'écrivain. Il a été renvoyé de l'université d'État de Moscou en 1975 et n'y a plus enseigné depuis. Cependant, il n'a pas été touché par de graves représailles à cette époque. La situation s'est aggravée lorsqu'en 1982, il a laissé le manuscrit de son essai "Russophobie", écrit en 1980, partir en "samizadat" : "Les vrais problèmes ont commencé lorsque j'ai écrit 'Russophobie'. ... J'ai écrit de nombreux ouvrages, mais c'est celui-là qui est vraiment célèbre. L'homme de la rue, si vous lui demandez qui est Shafarevich, serait capable d'associer mon nom exclusivement à cette œuvre.
Shafarevich lui-même pense que la principale chose qu'il a faite dans cet essai a été de généraliser le concept de "petites gens", qui a été introduit pour la première fois par l'historien français Augustin Cochin, qui a analysé la situation des cercles intellectuels en France avant la révolution de 1789 : "Cochin a décrit comment les "salons" français ont préparé la révolution. Elle a été réalisée par des personnes unies par un sentiment commun, à savoir le mépris et la haine de leur propre pays et de leur culture. Ils niaient toutes ses réalisations, considéraient la France et les Français comme quelque chose de peu de valeur par rapport à d'autres nations qui, selon eux, avaient remporté de grands succès, et insistaient sur le fait que seul un renversement radical dans tous les domaines de la vie ferait de la France "une partie de l'humanité éclairée". Les conséquences de leurs activités étaient terribles."
Shafarevich a suggéré qu'un tel phénomène - une "petite nation" - apparaît en période de crise majeure dans n'importe quel pays, qu'il s'agit d'une sorte de phénomène mondial. En tant que "petit peuple", Shafarevich voyait les sectes calvinistes protestantes en Angleterre pendant la Révolution anglaise du XVIIe siècle, les "illuminati" et les "encyclopédistes" en France à la veille de 1789, les "Hégéliens de gauche" en Allemagne, qui ont ouvert la voie à l'émergence du marxisme et de l'anarchisme, les nihilistes russes des années 1860 et 70... Ce sont ces minorités religieuses et idéologiques qui ont formé le noyau de la "contre-élite" et ont été la cause et le moteur de tous les grands cataclysmes sociaux qui se sont abattus sur les pays susmentionnés.

Le "petit peuple", dans l'interprétation de Shafarevich, n'est pas un courant national à proprement parler, car il pourrait inclure des représentants de différentes ethnies et nationalités. Cependant, à la veille des révolutions de 1905-1907 et de 1917 en Russie, ainsi que plus tard en URSS dans les années 1970 et 1980, "un certain courant de nationalisme juif" a joué un rôle majeur dans le "petit peuple".
C'est cette disposition qui a provoqué un grave conflit dans le mouvement social de l'époque, car dans la perception du camp dissident-libéral, elle permettait d'interpréter la "russophobie" comme un vulgaire pamphlet antisémite.
Au même moment, le KGB, alors dirigé par Yuri Andropov, a commencé à répandre des rumeurs sur l'arrestation possible du scientifique. Le début des années 1980 a été marqué par les arrestations et la persécution d'un certain nombre de membres du "Parti russe" de l'époque. Shafarevich se souvient de cette époque comme suit :
"Un document sur ce sujet est maintenant connu - la lettre d'Andropov au Politburo... Andropov y parle de certains "Russes" dangereux, qui sont apparus à la place de défenseurs des droits de l'homme vaincus. C'est à ce moment-là que la chasse aux personnes d'"obédience russe" a commencé. Ainsi, en 1982, L.I. Borodin a été arrêté. D'ailleurs, alors que l'enquête était déjà terminée, on lui a dit : "Votre sort est scellé. Voulez-vous savoir qui sera le prochain ? Shafarevich." Il a raconté cela à l'avocat, ce dernier à sa femme, sa femme à moi".
Néanmoins, Shafarevich n'a pas été arrêté, bien que la réaction à ce livre La russophobie soit encore tangible : sa femme a été suspendue de son enseignement à l'Institut d'ingénierie et de physique, et son fils n'a pas été admis au département de physique de l'Université d'État de Moscou.
Le conflit s'est particulièrement intensifié après la publication de l'essai en 1989 dans le journal "pseudo-romantique" Nash sovremennik. Des lettres collectives de protestation signées par Y. N. Afanas'ev, A. D. Sakharov, D. S. Likhachev, des mathématiciens américains, etc. se sont coalisés contre Shafarevich. En 1992, l'Académie nationale des sciences des États-Unis a appelé Shafarevich à refuser volontairement de devenir membre de l'Académie, car il n'existe aucune procédure d'expulsion de l'Académie (en 2003, Shafarevich l'a lui-même quittée en signe de protestation contre l'agression américaine contre l'Irak).
À partir de la fin des années 1980, Shafarevich a participé sporadiquement aux initiatives politiques et culturelles du mouvement national-patriotique alors naissant : on connaît sa participation symbolique à des organisations telles que l'Union nationale russe, l'Assemblée du peuple russe, le Front du salut national, le Parti démocratique constitutionnel-Parti de la liberté du peuple et le Centre panrusse de la droite nationale. Il a également contribué pendant un certain temps à des publications telles que le journal Den et le magazine Nash sovremennik.

Cependant, dans les années 1990 et au cours de la première décennie des années 2000, Shafarevich a joué son principal rôle public non pas en tant qu'homme politique, ce qu'il n'a jamais été, mais en tant qu'auteur d'interviews, d'articles et de livres, sans lesquels l'autodéfinition idéologique d'une partie du mouvement national conservateur moderne n'aurait pas été possible. Parmi eux, l'article "Deux routes vers un même précipice" mérite une mention spéciale, dans lequel le socialisme et le capitalisme sont considérés comme les hypostases d'une seule et même civilisation, dans laquelle tout ce qui est organique et naturel est étranger, tout est remplacé par un mécanisme complètement artificiel, où le rythme de travail et le style de vie sont subordonnés à la technologie, où tout est standardisé et unifié : la langue, les vêtements, les bâtiments.
Une telle civilisation est exceptionnellement productive à certains égards, comme sa capacité à nourrir sa population, à générer de l'énergie, à produire des armes de destruction massive, à contrôler et à manipuler la conscience de masse, etc. Mais cette civilisation, qui détruit activement la nature et supprime tous les aspects organiques et traditionnels de la vie, porte les germes de sa propre disparition, réduisant l'homme au plus bas niveau, celui de son essence animale. Cela doit inévitablement conduire à une crise spirituelle, démographique et écologique mondiale. La différence entre le mode de "progrès" occidental et le socialisme est que le premier est plus "doux" et repose davantage sur la manipulation de la conscience de masse, tandis que le second s'appuie incomparablement plus sur la violence directe et la coercition. Shafarevich a essentiellement appelé à la recherche d'une "troisième voie" qui mobiliserait l'expérience de toutes les formes de vie plus organiques pour surmonter la crise menant à la disparition de l'humanité.

La dernière œuvre majeure de Shafarevich est le traité "L'énigme des trois mille ans", consacré à la question juive, qu'il a écrit pendant vingt-cinq ans (c'est-à-dire depuis 1977).
L'idéologie de la "troisième voie", partagée par presque tous les courants conservateurs en Russie, a été développée en son cœur dans les écrits de Shafarevich, à commencer par son article programme "Deux routes vers un précipice" (1989). Le terme "russophobie", l'un des premiers utilisés par F.I. Tyutchev, a pris racine grâce à Shafarevich, d'abord dans le discours national-patriotique, et depuis environ 2014, il est fermement ancré dans la rhétorique officielle.
Shafarevich est décédé le 19 février 2017 et a été enterré au cimetière de Troekurovsky. En dépit de sa renommée nationale et internationale et de son prestige extrêmement élevé dans le milieu patriotique, dont certains avaient à cette époque réussi à s'engager de manière constructive avec l'establishment, il n'y a pas eu de condoléances de la part des autorités suprêmes, ni de reportages sur sa mort sur les chaînes de télévision centrales.
Principaux travaux de I.R. Shafarevich :
Shafarevich I. R. Socialism / I. R. Shafarevich // From under the boulders : a collection of articles. - M. : Paris : YMCA-PRESS, 1974. - С. 29-72.
Shafarevich I. R. Russophobia / I. R. Shafarevich. Œuvres complètes : en 6 vol. - Moscou : Institut de la civilisation russe, 2014. - VOL. 2 - P. 273-395.
Shafarevich I. R. Two roads to one precipice / I. R. Shafarevich. Collection complète des œuvres : en 6 volumes. - Moscou : Institut de la civilisation russe, 2014. - VOL. 2. - P. 3-54.
16:45 Publié dans Hommages | Lien permanent | Commentaires (0) | Tags : hommage, igor r. chafarevitch, russie, mathématiques, sciences, dissidence soviétique |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook
lundi, 15 janvier 2018
Spenglers duiding van wiskunde als cultuurfenomeen

Spenglers duiding van wiskunde als cultuurfenomeen
Verschillende cultuurzielen leveren verschillende soorten wiskunde op
door Emanuel Rutten
Welke rol speelt wiskunde in het denken van Spengler? In zijn hoofdwerk De ondergang van het avondland uit 1917 neemt de wiskunde ontegenzeggelijk een belangrijke plaats in. De titel van het eerste hoofdstuk – over de betekenis van getallen – verwijst er niet voor niets al naar.
Wiskunde is cultureel bepaald
Bekend is uiteraard dat volgens Spengler elke cultuur een bepaalde levenscyclus doormaakt en gekenmerkt wordt door een specifieke cultuurziel. Deze cultuurziel drukt zich uit op een groot aantal verschillende culturele en maatschappelijke terreinen. Alle cultuurfenomenen binnen een cultuur zijn ten diepste te begrijpen als veruitwendigingen of manifestaties van die ene cultuurziel die de gehele cultuur in kwestie bezield, draagt en in stand houdt.
Nu begrijpt Spengler de wiskunde eveneens als een cultuurfenomeen. Iedere cultuur drukt dus vanuit haar eigen verborgen ziel haar eigen wiskunde uit. Iedere cultuur heeft zijn eigen specifieke wiskunde precies omdat zelfs de wiskunde net zoals muziek, architectuur, politiek en alle andere cultuurfenomenen een uitdrukking is van de ziel van een cultuur. Zelfs de wiskunde is volgens Spengler dus een cultureel bepaald verschijnsel en niet universeel. Dit gaat uiteraard radicaal in tegen de gangbare Platoonse opvatting van wat wiskunde is.

De cultuurziel van de Griekse Oudheid
In zijn boek behandelt hij vervolgens de wiskunde van een aantal verschillende culturen. In wat volgt zal ik stilstaan bij twee daarvan, namelijk de wiskunde van de Griekse Oudheid oftewel de klassieke tijd en de wiskunde van het Avondland oftewel het Europese Westen. Om goed te begrijpen hoe deze twee zich tot elkaar verhouden dienen we op grond van het voorgaande dus eerst na te gaan hoe beide cultuurzielen zich precies tot elkaar verhouden.
Welnu, de ziel van de Griekse Oudheid is apollinisch. Ze wordt gesymboliseerd door het oersymbool van het zintuiglijk waarneembare individuele menselijke lichaam dat zich in een vaste, begrensde en welbepaalde onveranderlijke vorm in onze nabijheid voor ons bevindt. Deze typische gerichtheid op het menselijke waarnemen, op het “zien”, vinden we onder andere in de openingspassage van De Metafysica van Aristoteles. Daarin stelt hij dat alle mensen van nature streven naar weten en dat de mens het meest gehecht is aan het “zien” omdat we daarvan het meeste leren. De klassieke tijd wordt dus gekarakteriseerd door een hang naar concreetheid, naar het zintuiglijk aanschouwelijke, naar het eindige, naar het begrensde en naar de vaste vorm. In genoemd werk ontwikkeld Aristoteles dan ook een specifieke ‘vormen’-metafysica. Iets “is”, iets bestaat pas, doordat en omdat het een eindige afgeronde concrete vorm heeft. Het onbepaald vormloze, zoals volgens hem bijvoorbeeld het actueel oneindige, kan dan ook eenvoudigweg niet bestaan. Het vormloze staat anders gezegd gelijk aan het niets. Daarnaast is de klassieke oerziel gericht op “zijn” in plaats van op worden en op het in stand willen houden van een vaste natuurlijke orde in plaats van het voortdurend willen overschrijden van natuurlijk gegeven grenzen. Men heeft een sterke voorkeur voor het statische boven het dynamische en voor het discrete boven het continue.

De cultuurziel van het Avondland
Het oersymbool van de cultuurziel van het Avondland is daarentegen de abstracte oneindige, onmetelijke en onbegrensde ruimte. De Westerse cultuur is faustisch. Ze wordt gekenmerkt door het faustische streven naar oneindigheid en onmetelijkheid. Wat haar bezield is een enorme expansiedrift in ruimte en tijd. En dit ondanks dat deze abstracte oneindige ruimten haar ook een bepaalde angst kunnen inboezemen, zoals Pascal opmerkt in zijn Gedachten. De Westerse cultuur is steeds gericht op het abstracte, oneindige en onbegrensde. Men zoekt het vormloze en het onbepaalde. Ze wil in eerste instantie het intelligibele en niet het zintuiglijk waarneembare. Men wil “worden” in plaats van zijn. Het gaat voortdurend om het willen overschrijden van grenzen in plaats van om de gegeven natuurlijke orde in stand te houden. Ze heeft dan ook een sterke voorkeur voor het dynamische boven het statische en voor het continue boven het discrete.
Deze twee verschillende cultuurzielen leveren volgens Spengler twee volstrekt verschillende soorten wiskunde op. Eudoxis, Archimedes en Euclides waren wezenlijk andere wiskundigen dan Descartes, Leibniz en Newton, en later Euler, Lagrange, Poincare en Gauss.
 Apollinische antieke wiskunde
Apollinische antieke wiskunde
Uitgaande van haar oerziel wordt de apollinische antieke wiskunde gekenmerkt door de volgende aspecten. In de eerste plaats zijn getallen concrete meeteenheden voor het meten van de afmetingen en het volume van eindige voorwerpen die elk een welbepaalde en vaste vorm hebben. Daarnaast wordt de natuur gekenmerkt door volkomen harmonieuze onderling vergelijkbare verhoudingen. Al het waarneembare is anders gezegd ten opzichte van elkaar meetkundig commensurabel. Daarom erkent de apollinische wiskunde alléén gehele getallen en getallen die te schrijven zijn als verhouding van twee gehele getallen (i.e., breuken).
Alleen deze getallen representeren immers een harmonieuze maat. Het getal nul, negatieve getallen en irrationale getallen werden onverbiddelijk afgewezen omdat ze niet passen in de door hen veronderstelde harmonieuze orde van de natuur. Dergelijke getallen corresponderen niet met een eindige commensurabele vorm. Ze werden daarom tegennatuurlijk gevonden. Bekend is dan ook de legende uit de klassieke tijd dat de man die op een gegeven moment inzag dat de wortel van twee niet als breuk te schrijven is – en zo de irrationale getallen ontdekte – deze ontdekking vervolgens met de dood moest bekopen door op zee schipbreuk te leiden.
Zintuiglijk waarneembare bewijsvoering
Ten derde erkende de Griekse wiskunde geen actuele oneindigheden. Uitsluitend potentiële oneindigheden werden erkend. Actuele oneindigheden werden naar hun wezen verondersteld onbepaald en vormloos te zijn en dus onmogelijk te kunnen bestaan. Precies om deze reden wees men oneindig convergente rekenkundige reeksen – zoals de reeks 1/2+1/4+1/8+… met als limietsom het getal 1 – resoluut af. Een wiskunde van de limieten van dergelijke reeksen kwam dan ook niet van de grond. Ook werd om dezelfde reden het bestaan van een oneindig continuüm afgewezen. Want zo’n continuüm zou een actuele oneindigheid impliceren. En omdat actuele oneindigheden ontkend werden, werkte men nooit met oneindige verzamelingen van objecten, zoals de oneindige verzameling van alle driehoeken.
De aandacht richtte zich louter op één enkel concreet object, zoals een bepaalde driehoek die in de aanschouwing is gegeven. Iedere verdergaande abstractie werd geschuwd. In de vierde plaats was ook de wiskundige bewijsvoering altijd concreet en aanschouwelijk. Bewijsvoering diende plaats te vinden op grond van zintuiglijk waarneembare en uitvoerbare constructies en nooit op grond van een onthechte abstracte formele afleiding. Tenslotte maakte men om deze reden nooit gebruik van abstracte variabelen. Vanuit hun gerichtheid op het “statische” kende men meer in het algemeen géén dynamische wiskundige concepten zoals het moderne functiebegrip. Functies beelden de ene collectie entiteiten af op een andere en zijn dus te formeel en te dynamisch.
Faustische wiskunde
Uitgaande van haar oerziel wordt daarentegen de grensverleggende faustische wiskunde van het Avondland gekenmerkt door de volgende aspecten. Getallen worden geheel formeel en abstract begrepen als functies of als verzamelingen van verzamelingen. Het getal ‘drie’ wordt bijvoorbeeld strikt formeel gedefinieerd als de collectie van alle verzamelingen die in een één-op-één correspondentie te brengen zijn met de verzameling {a, b, c}. Zo ontstaat een zuiver abstract en onthecht getalbegrip.
De faustische wiskunde richt zich vanuit haar drang tot expansie en grensoverschrijding vervolgens op het ontwikkelen van zoveel mogelijk nieuwe soorten abstracte getallen. Naast het getal nul, de negatieve en de irrationale getallen kan hierbij gedacht worden aan complexe getallen, quaternionen, transcendentale getallen, kardinaalgetallen, ordinaalgetallen en infinitesimalen. De hechte band met de concreet gegeven empirisch waarneembare werkelijkheid die voor de Griekse wiskunde heilig was, wordt dus volledig losgelaten, ook al bleken later verrassend veel van deze nieuwe abstracte getallen zeer concrete toepassingen te hebben in de technische wetenschappen. Veel moderne technologische ontdekkingen zijn zonder deze nieuwe abstracte getallen zelfs onmogelijk.
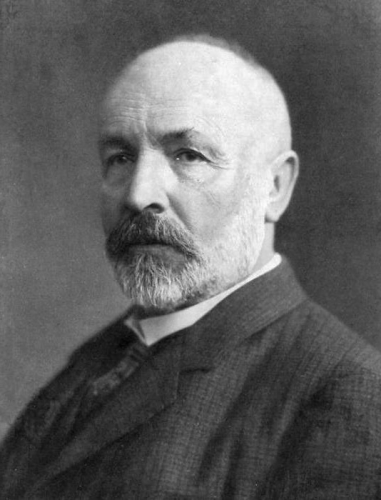
Wiskundige bewijsvoering werd formeel en abstract
In de tweede plaats erkent men volop het bestaan van actuele oneindigheden. Sterker nog, de wiskundige Cantor introduceerde een abstracte verzamelingenleer waarmee oneindig veel soorten oneindigheden ontsloten werden. Het aantal verschillende soorten oneindigheden bleek hierbij zelfs zo groot dat er niet aftelbaar maar zelfs overaftelbaar veel verschillende soorten oneindigheden zijn. De Duitse wiskundige Hilbert merkte na Cantors ontdekking dan ook op dat de moderne wiskunde zich nooit meer uit het door Cantor ontsloten paradijs zou laten verdrijven. In het verlengde hiervan begonnen de wiskundigen van het Avondland te werken met willekeurige oneindige verzamelingen van objecten in plaats van met één enkel object dat ons in de zintuiglijke aanschouwing gegeven is. Dit leidde tot een stormvloed aan nieuwe wiskundige ontdekkingen.
Ten derde werd wiskundige bewijsvoering volstrekt formeel en abstract. Ook in dit opzicht verbrak men dus de oude band met de concrete zintuiglijk waarneembare werkelijkheid. We kunnen hierbij denken aan de louter abstracte algebra en het inzetten van de zuiver formele rekenmethodes van de door Newton en Leibniz ontdekte integraal en differentiaalrekening. Daarnaast introduceerde men vanuit haar gerichtheid op het dynamische in tegenstelling tot het statische formele variabelen en abstracte functies. Het moderne functiebegrip had in de Oudheid dan ook nooit tot ontwikkeling kunnen komen. Tenslotte denkt men niet langer na over begrensde en eindige meetkundige figuren. De aandacht wordt volledig verlegd naar het analyseren van oneindige ruimten en abstracte oneindige structuren zonder directe concrete wetenschappelijke toepassingen. Dit resulteerde in een heel universum van nieuwe oneindige ruimten, zoals niet-Euclidische – , metrische – , Sobolev – , Banach – en Lebesque ruimten. Eveneens ontstonden allerlei nieuwe oneindige wiskundige structuren, zoals de structuren van de mathematische groepen –, Galois –, en categorieëntheorie.
Eeuwen wachten op oneindig convergente reeksen
Deze abstracte Westerse wiskunde zou door de concrete apollinische antieke cultuur gezien worden als een ernstige, ja zelfs perverse, ontaarding en ontkenning van het primaat van de harmonische natuurlijke orde. Men zou het hebben afgedaan als onthecht, onnatuurlijk, niet reëel en illusoir. Dit pathos van de Griekse cultuurziel heeft er echter wel voor gezorgd dat zij zich nooit zo sterk expansief heeft kunnen ontwikkelen als in het Avondland. Vele belangrijke paradoxen, zoals die van Zeno, zijn voor de Griekse wiskunde altijd onoplosbaar gebleven. En dit precies omdat zij de faustische wiskundige concepten die nodig zijn voor het oplossen ervan – zoals in dit geval oneindig convergente reeksen – nooit heeft kunnen overwegen en aannemen. De mensheid moest na de Griekse Oudheid dan ook nog vele eeuwen wachten voordat de wiskunde van het Avondland deze en andere problemen eindelijk zou oplossen.
00:55 Publié dans Philosophie, Révolution conservatrice, Science, Sciences | Lien permanent | Commentaires (0) | Tags : oswald spengler, mathématiques, mathématiques grecques, mathématiques faustiennes, révolution conservatrice, allemagne, philosophie, esprit grec, esprit apollinien, esprit faustien |  |
|  del.icio.us |
del.icio.us |  |
|  Digg |
Digg | ![]() Facebook
Facebook


